I was reading Twitter/X the other day when I came across a compelling question from Kevin Naughton:
someone pls explain how hashing algorithms like SHA-256 are irreversible like i’m 5 years old
— Kevin Naughton Jr. (@KevinNaughtonJr) September 24, 2023
This is a wonderful question and, to be honest, something I didn’t understand until a few years ago when I wrote part 2 of The Imposter’s Handbook.
As you can see, Kevin got a lot of replies and, if I’m honest, there seems to be a lot of confusion. Old Rob might take up the challenge here, striking up some exciting conversation on Twitter about the nature of one-way functions… but let’s be positive and dig in to some details.
The Enemy Knows the System
There are a lot of very wrong replies to Keven’s tweet and I don’t want to call anyone out, but I will say that the theme of wrongness goes something like this:
I have a bunch of things and if I scramble those things up and give them to you, you’ll have no way to unscramble them.
There were examples of candy, cake, a deck of cards, and so on and many of them made sense in a human way. I wouldn’t want to unshuffle a deck of cards or unbake a cake!
But see here’s the thing: if I know the result (a lovely cake) and your exact process, which I will because these are algorithms after all that must produce the exact same result - then it’s possible for me to figure out the initial ingredients - easily I might add. It might take a while and some guessing, but in short order I will produce the exact same cake.
When you bake a cake or shuffle cards, you’re doing encryption: turning one value into another following a process.
Hashing, on the other hand, is completely different. Hashing turns some value into an unrelated number using functions that you can’t reverse - this last bit is the thing I think most commenters were missing.
What’s a One-way Function?
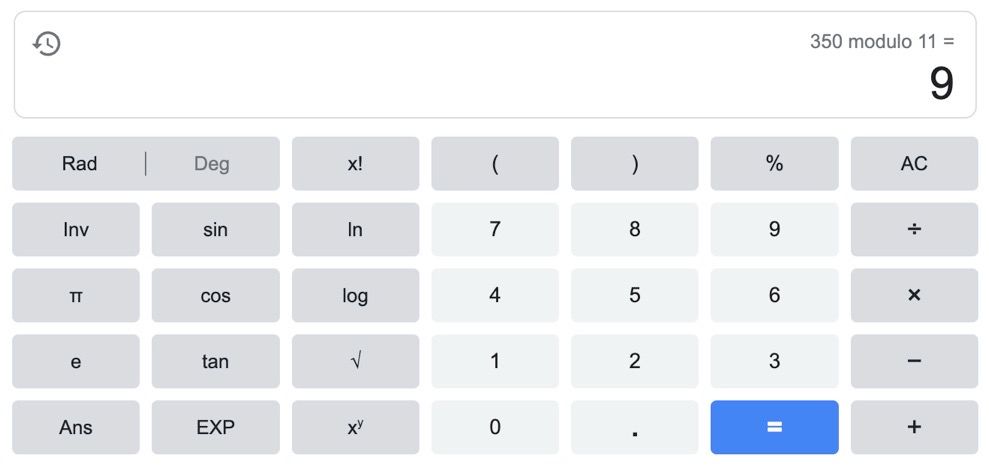
Let’s take our cake’s individual ingredients and weigh them on a scale that only counts up to 11 grams and then starts again at 0:

Some ingredients will weigh more than 11 grams, of course, but you would still record the number you see on the dial. For instance: 35o grams of flour would spin this dial around quite a few times before ultimately landing on the number 9.
This is a modular operation; 350 mod 11 to be specific:
350 mod 11
Now, imagine that I do the same for every ingredient and record what the dial says using my mod 11 scale, and then write that number down. It might end up being something like:
Sugar: 4
Flour: 9
Eggs: 3
Oil: 3
Vanilla: 10
Milk: 3
Salt: 0
Butter: 8
Baking Powder: 4
Now we have a number we can play with, or compress, in our hashing algorithm: 4933103084. How did we get this number? Well you just saw me do it, but there’s no way you could reliably figure out my ingredients list from here!
Hey, It’s a Video!
Want to see more? I made a video about all of this and I do hope you enjoy…